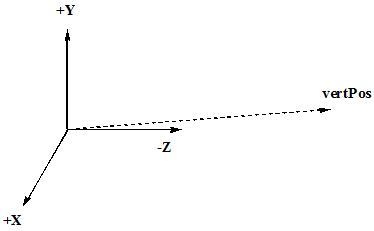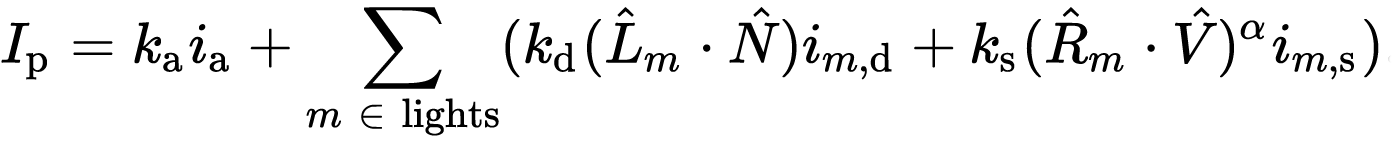Phong Lighting Model - explained

The Phong reflection model, developed by Bui Tuong Phong in 1975 (my last year in high school), is a widely used mathematical model in computer graphics for the calculation of the color of pixels on an object's surface. It takes into account three components: ambient, diffuse, and specular reflection, as well as a specular exponent, in order to accurately simulate the way light interacts with surfaces.

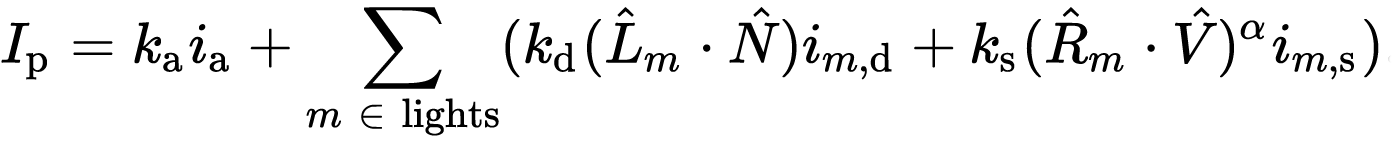
The ambient reflection component represents the color of an object when not directly illuminated by any light sources. It is determined by the product of the surface's ambient color and the ambient color of the light source, anything in shadow.

The diffuse reflection component represents the color of an object when illuminated by a light source. It is determined by the product of the surface's diffuse color, the diffuse color of the light source and the cosine of the angle between the surface normal and the light direction.

The specular reflection component represents the color of an object when illuminated by a light source and viewed from a certain angle. It is determined by the product of the surface's specular color, the specular color of the light source and the cosine of the angle, raised to the power of the specular exponent.

The specular exponent, also known as shininess, is a value that controls the size and intensity of the specular highlight on the surface. The higher the specular exponent, the smaller and more intense the specular highlight will be.

Starting with the vertex shader

#version 450
#extension GL_ARB_separate_shader_objects : enable

layout(location = 0) in vec4 vVertex;
layout(location = 1) in vec3 vNormal;
layout(location = 2) in vec2 uvCoord;

uniform mat4 modelMatrix;
uniform mat4 viewMatrix;
uniform mat4 projectionMatrix;
uniform vec3 lightPos;

layout(location = 0) out vec3 vertNormal;
layout(location = 1) out vec3 lightDir;
layout(location = 2) out vec3 eyeDir; 


void main() {
    mat3 normalMatrix = mat3(transpose(inverse(modelMatrix)));
    vertNormal = normalize(normalMatrix * vNormal); /// Rotate the normal to the correct orientation 
    vec3 vertPos = vec3(viewMatrix * modelMatrix * vVertex);
    vec3 vertDir = normalize(vertPos);
    eyeDir = -vertDir;
    lightDir = normalize(vec3(lightPos) - vertPos); 
    gl_Position = projectionMatrix * viewMatrix * modelMatrix * vVertex;
    
}

Let's discect just the math part of the new code.
vec3 vertPos = vec3(viewMatrix * modelMatrix * vVertex);
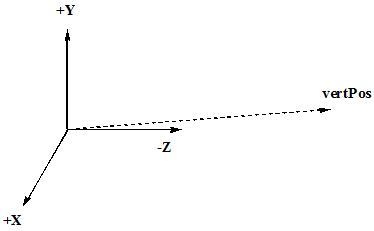
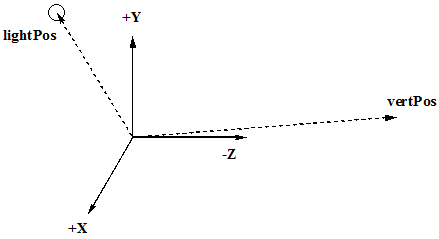
Smiley face
In this line multiply the vertex by the model matrix and the view matrix. This will push the vertex away from the origin. Remember the camera is aways at the origin looking down the -Z axis. In many books and websites they refer to this as eyePos but really it is the vertex position from the eye. If the this vector is negated (-vertPos), I agree it is the eyePos but only from the point of view of the now shifted vertex. Too complicated for me.
The call to vec3(...) is a typecast to convert the resulting vec4 to a vec3 we no longer need the be in 4-D.

The light source is not altered by any of the matrix transformations, so it position remains the location passed by the uniform lightPos.
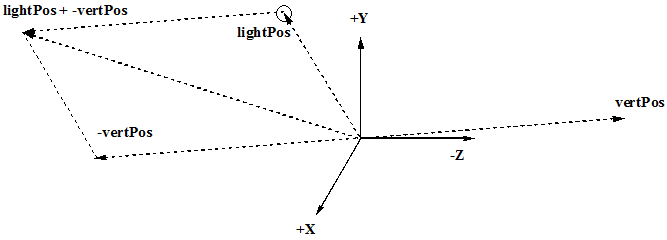
Smiley face

What is needed now is to calculate the position of the light source with respect to the new position of the vertex. By subtracting the the lightPos fron the vertPos (add the lightPos to the negative of the vertPos).
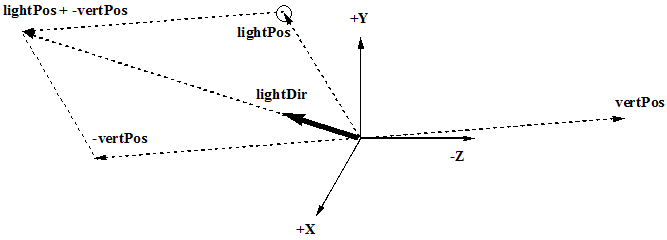
vec3 vertPos = vec3(viewMatrix * modelMatrix * vVertex); Smiley face

Normalizing the lights position gives the lightDir from the point-of-view of the, matrix shifted, vertex. The lightDir will be passed to the fragment shader.

Smiley face

Now the fragment shader

#version 450
#extension GL_ARB_separate_shader_objects : enable

layout(location = 0) out vec4 fragColor;

layout(location = 0) in vec3 vertNormal;
layout(location = 1) in vec3 lightDir;
layout(location = 2) in vec3 eyeDir; 

void main() {
    vec4 ks = vec4(0.3, 0.3, 0.3, 0.0);
	vec4 kd = vec4(0.6, 0.6, 0.3, 0.0);
	vec4 ka = 0.1 * kd;
	float diff = max(dot(vertNormal, lightDir), 0.0);

	/// Reflection is based incedent which means a vector from the light source
	/// not the direction to the light source
	vec3 reflection = normalize(reflect(-lightDir, vertNormal));
	float spec = max(dot(eyeDir, reflection), 0.0);
	spec = pow(spec,14.0);
	fragColor =  ka + (diff * kd) + (spec * ks);	
}

I'm bringing everything in as a vec3 since we no longer need to worry about 4-D homogenious coordinate systems. The final color still needs to be a vec4.
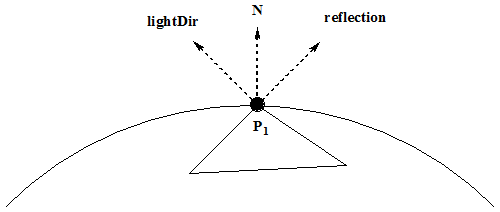
Since this is the fragment shader, the code is being run on a per-pixel level. So, given a pixel P₁, on some triangle, the normal to the surface at that point is N and the lightDir vector is drawn below. The drawings I'm providing are a "lying" version of the story. None of the vectors, except the vertex are "at the vertex position" they are really ate the origin but remember, they are directional vectors only, so my pictures, although technically wrong, is painting a correct picture.
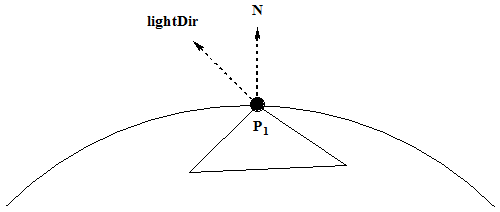
Smiley face
The amount of diffused light on the surface is equal to the cos() between the normal to the surface and the lightDir - the dot product.
float diff = max(dot(vertNormal, lightDir), 0.0);
The dot product between the two vectors will go between 1.0 and -1.0. The max() function keeps all the values positive or zero.

Calculating the relection vector of the lightPos off the surface defined by the normal, the direction of the reflecting off the surface can be created.
vec3 reflection = normalize(reflect(-lightDir, vertNormal));
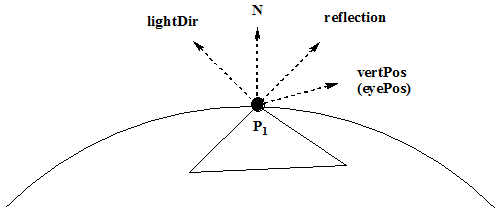
Smiley face
Because I'm basing this math at the vertex position (a big lie), this next bit is harder to see. To find the specular value I need to take the dot product of the refletion vector with the eyeDir but is really the vertexPos is the negative of the eyePos from the vertex prespective so reverse it again. Therefore, the eyePos is the vertPos.
float spec = max(dot(eyeDir, reflection), 0.0); Smiley face

The last part is raising the spectular component to a power, spec^exponent. This is just artistic and has nothing to do with physics. The higer the exponent, the "shinnier" the surface.
spec = pow(spec,14.0);